
Данный алгоритм по решению судоку 9x9 прислал наш регулярный игрок Александр Кузнецов (alex_tlt)
Предлагаю вниманию любителей судоку свой алгоритм решения этой увлекательной задачи. Сразу оговорюсь, что алгоритм не самый быстрый, а некоторые приёмы решения сознательно опущены.
Моя цель – показать алгоритм, то есть, последовательность действий, которая обязательно приведёт к успеху.
В качестве примера используется судоку № 3448. Алгоритм состоит из четырёх пунктов.
1. Если в строке, столбце или квадрате заполнены 8 клеток, то в девятую, пустую клетку надо вписать недостающую цифру. Если при этом окажется, что в большом квадрате 9х9 пустых клеток не осталось, судоку считается решенным. Этот пункт не требует иллюстраций, его я включил только лишь для соблюдения полноты алгоритма.
2. Квадрат выгодно отличается от строк и столбцов своей компактностью. Поэтому целесообразно начинать решение именно с квадратов. Выбираем любую цифру от 1 до 9 и мысленно проецируем заполненные цифры на те квадраты, в которых выбранной цифры нет. Предпочтительнее начинать с самой часто встречающейся в условии цифры. Если же не учитывать этот фактор, начинаем с цифры 1.
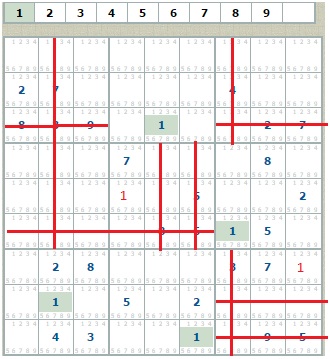
Четыре единицы (они выделены фоном)  проецируются на 5 квадратов, не содержащих эту цифру. Сразу же обнаруживаются единственные пустые клетки в среднем квадрате и нижнем правом квадрате.
проецируются на 5 квадратов, не содержащих эту цифру. Сразу же обнаруживаются единственные пустые клетки в среднем квадрате и нижнем правом квадрате.
Заполняем эти клетки единицами:
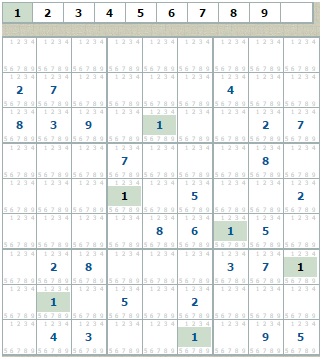
Продолжаем поиск в оставшихся квадратах цифры 1 с учётом найденных.
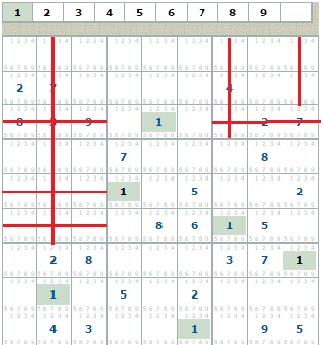
Новых единиц не найдено. Переходим к следующей цифре 2, будет найдена одна двойка. Рисунок не привожу, чтобы не загромождать документ. Переходим к следующим цифрам, будут найдены тройка, пятёрка, семёрки. Что касается восьмёрок, иллюстрация просто необходима!
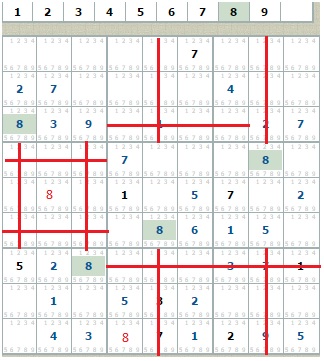
Четыре восьмёрки проецируются на 5 квадратов, не содержащих эту цифру. Единственные пустые клетки обнаруживаются в нижнем среднем квадрате и в среднем левом. Причём последний – совершенно пуст! Это ещё раз подчёркивает высказанное ранее положение о компактности квадратов. В нашем случае достаточным оказалось четыре цифры, чтобы закрыть восемь пустых клеток.
Далее, после поиска цифры 9 судоку приобретает следующий вид:
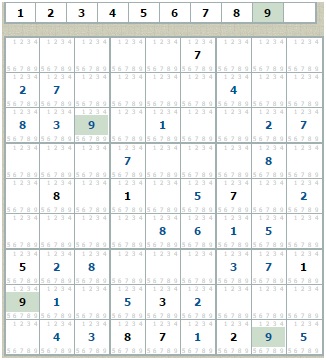
Теперь необходимо применить пункт 1 (его всегда нужно держать в уме) последовательно для самой нижней строки, где недостаёт шестёрки, а затем для нижнего левого квадрата, где недостаёт семёрки.
Возвращаемся к пункту 2 и возобновляем поиск с цифры 1. В данном алгоритме пункт 2 должен закончиться только тогда, когда перебор всех 9-ти цифр не даст ни единого положительного решения.
Переходим к пункту 3.
3. В третьей сверху строке остались незаполненными три клетки-кандидата с цифрами 4, 5, 6 (серые цифры). В шестом столбце уже есть 5 и 6, следовательно остается вариант 4 - последний кандидат.
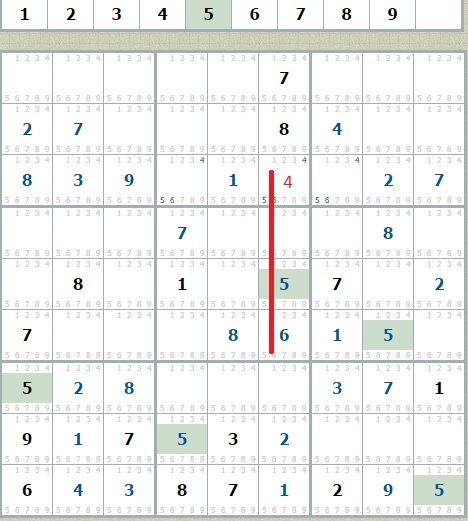
Сложные судоку, как правило, не обходятся без пункта 4 «Альтернативы». Разберём этот случай применительно к судоку № 3448, допустив что на определённом этапе мы не смогли обойтись п.п. 1-3.
4. В самом левом столбце остались незаполненными две клетки, значения которых могут быть либо 1, либо 4, и они отмечены серыми цифрами. В этом случае предполагаем, что 1 находится в верхней клетке и нажимаем кнопку «Сохранить».
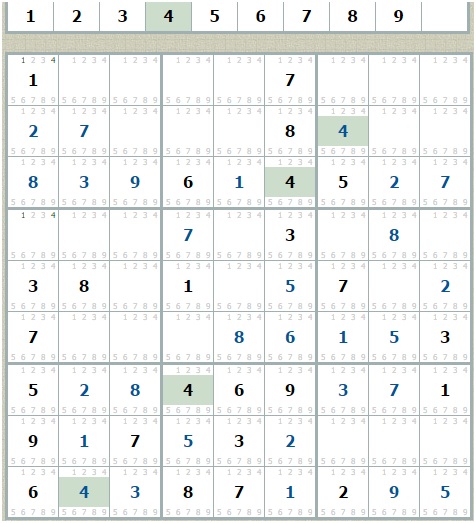
После того, как судку сохранен, в альтернативной клетке ставим 4 и выполняем пункт 2 «Поиск по квадратам».
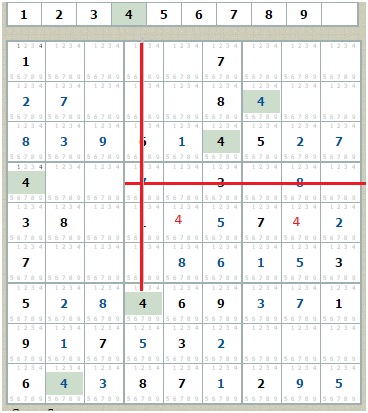
В результате приходим к противоречию: пятая сверху строка содержит две одинаковые цифры 4. Замечу, что при решение альтернатив противоречие является наиболее желаемым результатом! Теперь остаётся нажать кнопку «Загрузить» и в сохранённом судоку в верхней клетке вместо 1 поставить 4, а в альтернативной 1.
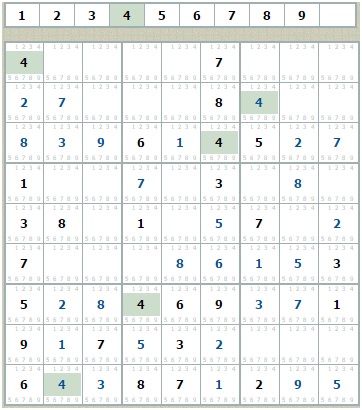
А далее опять повторение пунктов 1-3, которые приведут к правильному решению. Удачи!
 0
0
 3
3